Verilog编程-4. 有符号整数加减法
1. 背景
在Verilog中,对于有符号数的操作总是有很多迷惑的地方,例如加法怎样看是否溢出,进位有什么用,Verilog中 + 的本质是什么,减法器怎么设计,如果使得计算具备完整性等等。通过具体的程序来解答这些问题。
2. 加法器设计思路
首先需要明确的是,Verilog中的 + 是进行二进制的加法,遵循的是最基本的加法定律,如下图所示
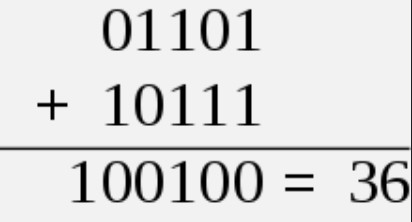
2.1. 进位和结果
而有无符号是我们自己的定义,本质上在数字电路中,都是进行的以上的加法,即1+0=1, 1+1=0然后进1。当我们人为地定义最高位为符号位之后,加法才有了一些限制和变化。下面是最基础的有符号加法器的程序语句:
assign {ca, result} = a + b;
其中 ca 是加法进位,result 是除去进位加法剩余的部分,也就是加法的和。
2.2. 溢出
对于二进制加法,还需要考虑溢出的问题,因为二进制的位数是有限的。对于有符号数的加法,使用如下程序语句判断是否溢出:
assign overflow = (a[n-1]==b[n-1] && result[n-1]!=a[n-1]);
其判断原理是:如果两个参加加法运算的变量符号相同,而运算结果的符号与其不相同,则运算结果不准确,产生溢出。即两个正数相加结果为负数,两个负数相加结果为正数,肯定是溢出了。而一正一负两个数相加是不会产生溢出的。
而对于溢出和进位应该如何考虑呢?首先如果没有发生溢出,那么就不用看进位了,计算得到的结果 result 就是正确的结果;如果发生了溢出,这个时候就要把进位加上,放在 result 的前面,组成 {ca, result} ,此时 ca 作为符号位,这样的结果才是正确的。或者说在真实Verilog计算中,如果发生了溢出,那么单有 result 的结果肯定是不正确的。如下程序块所示:
a = 4'b0011;
b = 4'b1100;
{ca, result} = a + b; // ca=0, result=4'b1111
overflow = (a[3]==b[3] && result[3]!=a[3]); // overflow=0
此时未发生溢出,a的十进制数值为3,b的十进制数值为-4,两者相加为-1,其二进制表达刚好为 4'b1111 。如果程序块如下所示:
a = 4'b1011;
b = 4'b1101;
{ca, result} = a + b; // ca=1, result=4'b1000
overflow = (a[3]==b[3] && result[3]!=a[3]); // overflow=0
此时没有发生了溢出,那么最终得到的结果应该是 {result},即 4'b1000 。而a的十进制数值为-5,b的十进制数值为-3,两者相加正好是-8,即 4'b1000 。在再看下一个例子:
a = 4'b1001;
b = 4'b1101;
{ca, result} = a + b; // ca=1, result=4'b0110
overflow = (a[3]==b[3] && result[3]!=a[3]); // overflow=1
此时已经发生了溢出,所以最终得到的结果应该是 {ca, result},即 5'b10110 。a的十进制数值为-7,b的十进制数值为-3,两者相加为-10,即 5'b10110。
2.3. 判断是否为0
使用如下程序语句,就可以判断结果是否为0:
zf = ~(|result);
3. 减法器设计思路
在实际的运算器中,如果参与运算的操作数都是补码的话,可以用加法器同时实现加法和减法。即先对减数取反加1,然后再将其和被减数使用加法器加和即可。其他情况和加法器雷同。需要注意的一点是,如果减法运算中减数是最小负数时候,溢出判断需要特殊处理。一般情况下,溢出判断时需要取反加1之后的最高位进行判断;如果减数是最小负数时,溢出判断需要取反之后的最高位,而不是取反加1之后的最高位。对于4位减法来说,程序如下所示:
assign temp = ~b + 1;
assign overflow = (b==4'b1000) ? (a[3]==~b[3] && result[3]!=a[3]) : (a[3]==temp[3] && result[3]!=a[3]);
4. 代码
整个工程包括 adder.v,suber.v 源文件,top_tb.v 仿真文件,top.f 文件列表文件以及 Makefile 文件。文件编辑平台是 vscode, 仿真平台是Ubuntu系统下的VCS,波形显示软件是Verdi。具体文件内容如下所示。
adder.v
module adder (
input [3:0] a, b,
output ca,
output [3:0] result,
output overflow,
output zf
);
// 这种方法对于有符号数来说是正确的,获得进位,结果,是否溢出以及0判断是正确的
assign {ca, result} = a + b;
assign overflow = (a[3]==b[3]) && (result[3]!=a[3]);
assign zf = ~(|result);
endmodule
suber.v
module suber (
input wire [3:0] a, b,
output ca,
output [3:0] result,
output overflow,
output zf
);
wire [3:0] temp;
assign temp = ~b + 1;
assign {ca, result} = a + temp;
assign overflow = (b==4'b1000) ? (a[3]==~b[3] && result[3]!=a[3]) : (a[3]==temp[3] && result[3]!=a[3]);
assign zf = ~(|result);
endmodule
top_tb.v
如果需要仿真加法器模块,将实例化中的 suber 模块换成 adder 模块即可。
module top_tb;
reg [3:0] a, b;
wire [3:0] result;
wire ca;
wire overflow;
wire zf;
suber uut1(
.a (a),
.b (b),
.result (result),
.ca (ca),
.overflow (overflow),
.zf (zf)
);
initial begin
integer i,j;
for (i=0; i<16; i=i+1) begin
for (j=0; j<16; j=j+1) begin
#5 a = i; b = j;
end
end
#50 $finish;
end
`ifdef FSDB
initial begin
$fsdbDumpfile("top.fsdb");
$fsdbDumpvars();
end
`endif
endmodule
Makefile
.PHONY: sim, verdi, clean
PROJECT = top
VCS = vcs \
-R \
-timescale=1ns/1ps \
-debug_all \
-fsdb \
+define+FSDB \
-full64 \
+v2k \
-sverilog \
VERDI = verdi \
-sv \
-nologo \
-ssf ${PROJECT}.fsdb \
sim:
make clean
${VCS} -f ${PROJECT}.f
verdi:
${VERDI} -f ${PROJECT}.f &
clean:
rm -rf ./csrc ./DVEfiles *.daidir *.log simv* *.key *.vpd \
verdi* novas* *.fsdb
top.f
./adder.v
./suber.v
./top_tb.v
5. 仿真结果
对加法器的仿真结果图 
对减法器的仿真结果图 
文档信息
- 本文作者:Polaris
- 本文链接:https://polaris-chn.github.io/2022/04/15/Verilog-practice-4/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)
