Verilog编程-8. 线性反馈移位寄存器 LFSR

背景和原理

线性反馈移位寄存器（LFSR, Linear Feedback Shift Register）通常用于循环冗余校验的特征分析以及伪随机二进制的产生，在介绍LFSR的原理之前，首先需要介绍模2运算和模2多项式。

模2运算

模2运算是一种二进制算法，包括模2加（+）、模2减（-）、模2乘（×或·）、模2除（÷或/）四种二进制运算。与四则运算不同的是模2运算不考虑进位和借位，即模2加法是不带进位的二进制加法运算，模2减法是不带借位的二进制减法运算，这样两个二进制位相运算的时候，两个位的值即可确定运算结果，不受前一次运算的影响，也不对下一次运算造成影响（本质上可以看成两个二进制按位异或的操作，加减都是这样）。下图分别是模2加法和模2减法的简单示意图。

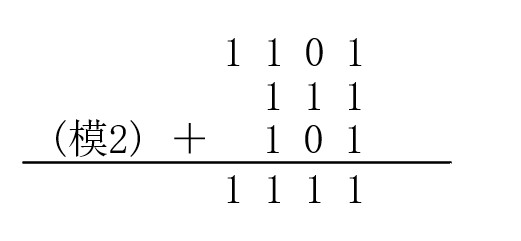
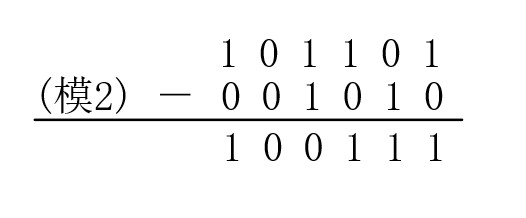
可以看出模2加法和模2减法是一回事，完全一样。并且通过按位异或的角度来看，模2加中奇数个1相加得1，偶数个1相加得0，这个结论在奇偶校验中很有用。

多位数的模2乘法和普通乘法演算是一样的，唯一的区别就是，部分积相加时按模2加。简单的示意图如下所示。

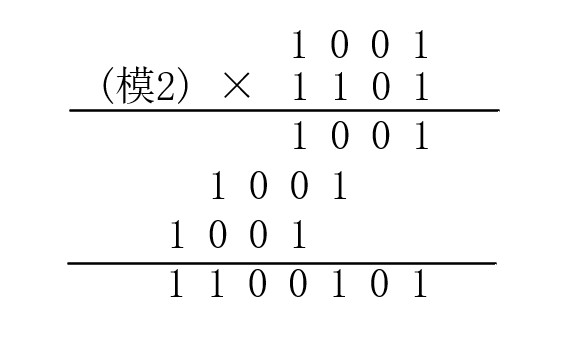
模2除法是模2乘法的逆运算，其具有三个性质： （1）当最后余数的位数小于除数位时候，除法停止； （2）当被除数的位数小于除数位数时候，则商数为0，被除数就是余数； （3）只要被除数或部分余数的位数与除数一样多，且最高位为1，不管其他位是什么数，皆可商1；

下面是模2除法的一个简单示意图。

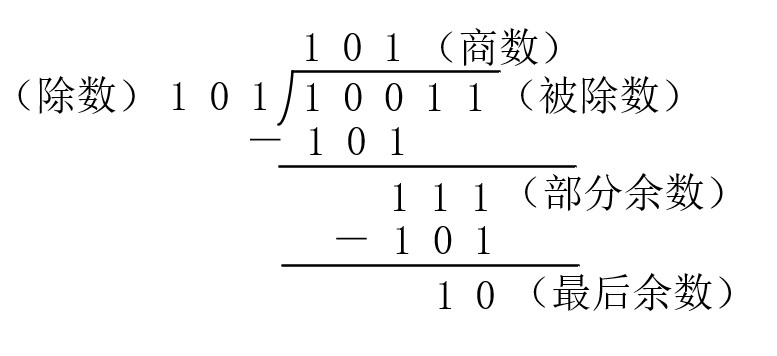
模2运算成为计算机、通信、编解码等学科的重要数学基础，在数字编码、数据校验等理论方面有重要应用。模2运算是编码理论中多项式运算的基础，下面就介绍模2多项式的概念和运算规则。

模2多项式

采用模2运算规则的多项式称之为模2多项式。通用的模2多项式为：P(x)=a_nx^n+a_(n-1)x^(n-1)+…+a_1x^1+a_0x^0。该多项式有以下规定：

（1）多项式由多个分项组成，分项是由变量x的幂及其对应系数的积组成，幂n表示了每个分项在多项式中不同的位置，各个分项之间没有权值的关系；

（2）x仅表示变量，仅是用x的幂区分不同分项，x_n没有数值的含义；

（3）x_0=1，所以最后一项可以直接写成 a_0;

（4）系数a_n, a_(n-1), …, a_0是二值数域，即只有0或1两个值；

（5）多项式模2运算满足交换律，结合律和分配律；

对于模2多项式的计算，可以参照上述的模2运算。例如，P1(x)=x^3+x^2+x^1+1，P2(x)=x^2+1，P(x)=P1(x)+P2(x)。由于两个多项式的系数分别为1111和0101，所以两个多项式相加即为多项式系数进行模2加法，结果为1010，所以P(x)=x^3+x^1。其他的模2多项式减法，乘法和除法，也都是类似的。

LFSR原理

LFSR通常由移位寄存器和异或门逻辑组成，其主要应用在：伪随机数，伪噪声序列，计数器，BIST，数据的加密和CRC校验等。LFSR主要包括两大类：斐波那契（外部LFSR，又称many-to-one）和伽罗瓦（内部LFSR，又称one-to-many）。下图分别为伽罗瓦LFSR和斐波那契LFSR。其中：

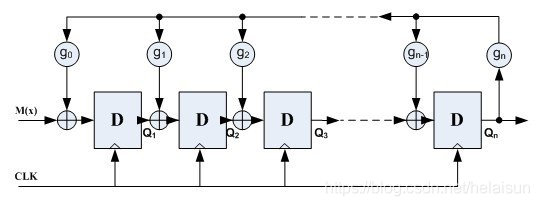
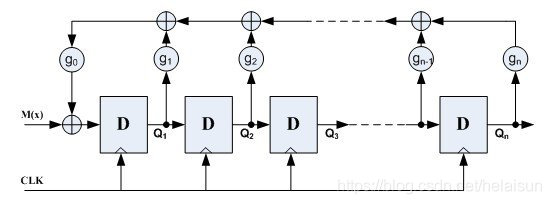
（1）gn为反馈系数，取值只能为0或1，取0时表示不存在该反馈路，取1时表示存在该反馈路；这里的反馈系数决定了产生随机数的算法不同。用反馈函数表示成G(x)=gnx^n + … + g1x^1 + g0，这个既可以是反馈函数，也可以是LFSR的结构，即生成多项式。反馈函数为线性的叫线性反馈移位序列，否则叫非线性反馈移位序列；

（2）Qn为LFSR的输出，M(x)是输入的码字多项式，如M(x)=x^4 + x^1 + 1，表示输入端的输入顺序为11001；

下面是一个生成多项式为G(x)=x^8 + x^6 + x^4 + 1的两种LFSR的具体实例，如下图所示。

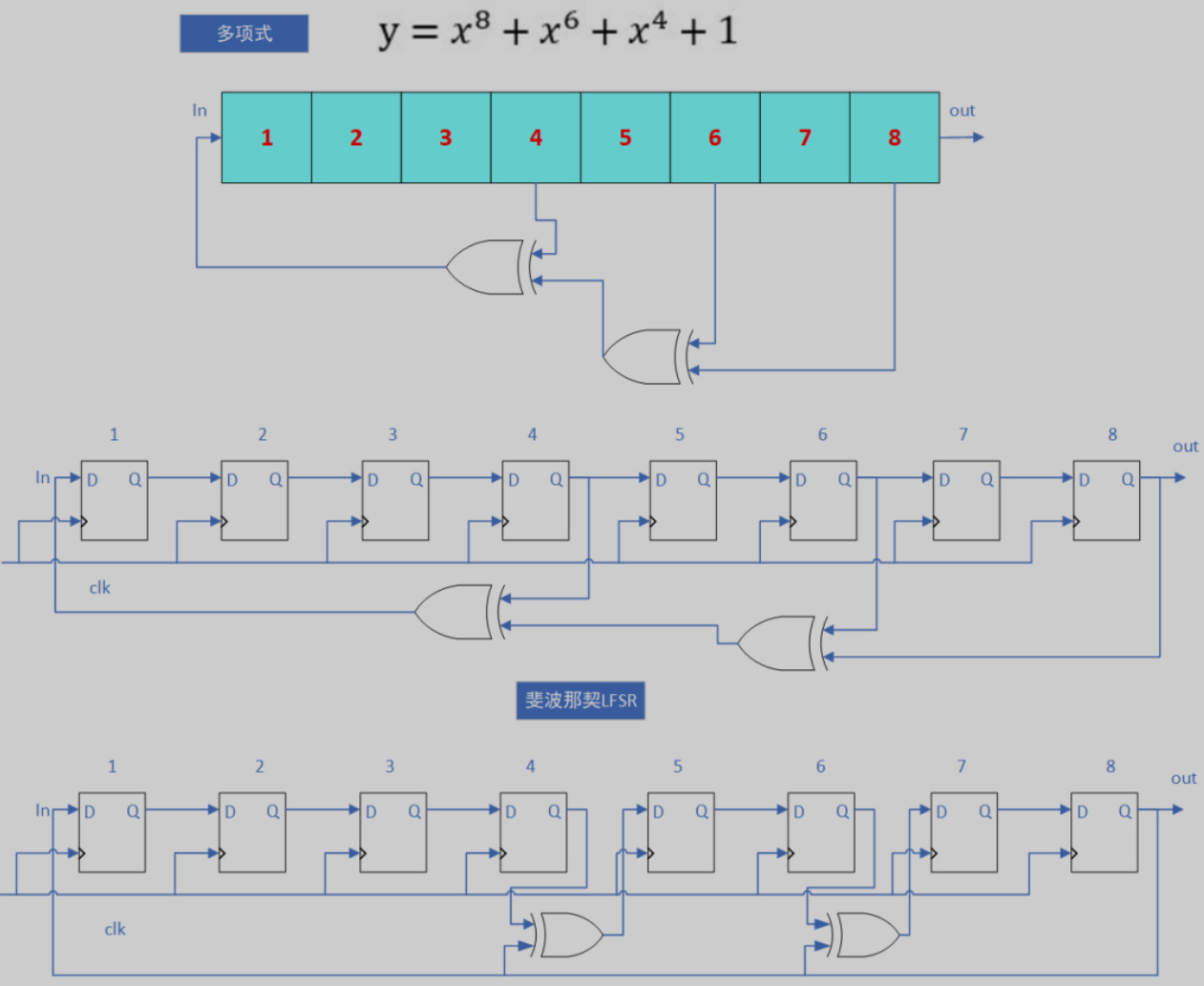
影响线性反馈移位寄存器的下一个状态的比特位叫做抽头，选取的某些位构成的序列就是抽头序列。n个D触发器可以提供2^n-1个状态（除去全0状态，LFSR会陷入死循环），为了保证这个最长的周期，抽头序列的多项式加1必须是一个本原多项式，即不可约（就是不可以分解，不可以写成多个多项式相乘的形式），例如：G(x)=x^4 + x + 1。

LFSR的初始状态是由传入的码字多项式提供的；并且当反馈系数不同时，得到的状态转移图也不同；必须保证gn==1，否则就没有反馈了；D触发器的个数越多，产生的状态就越多，也就越“随机”；如果真的进入到全0状态，那就经过~|Q[n-2:0]^Q[n-1]（这里是先或再取反再异或），这样逻辑运算后输出的结果为1，保证线性反馈器不会陷入到死循环。

设计思路

使用Verilog实现上图中生成函数为 G(x)=x^8 + x^6 + x^4 + 1 的伽罗瓦LFSR，其初始状态为8’b1001_1101。根据背景和原理介绍，LFSR主要由移位寄存器和异或门逻辑组成，将特定的抽头的比特位进行异或逻辑，就可以得到某一位的下一个状态了。

代码

工程文件由源文件lfsr.v，仿真文件lfsr_tb.v，Makefile文件makefile和文件列表文件lfsr.f组成。编辑平台为vscode，仿真平台为vcs，波形查看平台为verdi。具体程序如下：

lfsr.v

module lfsr (
    input clk,
    input rstn,
    output reg q
);

// 移位寄存器
reg [7:0] sr;
always @(posedge clk or negedge rstn) begin
    if (!rstn)
        sr <= 8'b1001_1101;
    else begin
        sr[7]   <= sr[6];
        sr[6]   <= sr[5] ^ sr[7];
        sr[5]   <= sr[4];
        sr[4]   <= sr[3] ^ sr[7];
        sr[3]   <= sr[2];
        sr[2]   <= sr[1];
        sr[1]   <= sr[0];
        sr[0]   <= sr[7];
    end
end


always @(posedge clk or negedge rstn) begin
    if (!rstn)
        q <= 0;
    else
        q <= sr[7];
end
// assign q = sr[7];

endmodule

lfsr_tb.v

module lfsr_tb;
    reg clk;
    reg rstn;
    wire q;

    lfsr uut (
        .clk    (clk),
        .rstn   (rstn),
        .q      (q)
    );

    initial begin
        clk = 0;
        rstn = 0;
        #20 rstn = 1;
    end

    initial begin
        forever #5 clk = ~clk;
    end

    initial begin
        #300 $finish;
    end

    `ifdef FSDB
    initial begin
        $fsdbDumpfile("lfsr.fsdb");
        $fsdbDumpvars();
    end
    `endif 


endmodule

Makefile

.PHONY: sim, verdi, clean

PROJECT = lfsr

VCS =	vcs \
		-R \
		-timescale=1ns/1ns \
		-debug_all \
		-fsdb \
		+define+FSDB \
		-full64 \
		+v2k \
		-sverilog \

VERDI =	verdi \
		-sv \
		-nologo \
		-ssf ${PROJECT}.fsdb \


sim:
	make clean
	${VCS} -f ${PROJECT}.f


verdi:
	${VERDI} -f ${PROJECT}.f &

clean:
	rm -rf ./csrc ./DVEfiles *.daidir *.log simv* *.key *.vpd \
				verdi* novas* *.fsdb

lfsr.f

./lfsr.v
./lfsr_tb.v

仿真结果

在初始状体为8’b1001_1101的情况下，其输出应该为1, 0, 1, 1, 1, 0…，下图是仿真显示的波形图，由图中可知，仿真结果显示正确。